데이터를 바탕으로 어떤 model을 구축한다고 할 때, 1) model을 먼저 가정하고, 2) 그 model의 parameter를 찾아야 한다. 이때 model parameter를 estimation하는 방법으로 MoM (Method of Moments)와 MLE (Maximum likelihood estimation)가 있다. MLE가 특히 consistent한 estimator 중 가장 optimum하다고 알려져 있는데 (estimator의 분산이 가장 작음), 이 포스팅에서는 MLE에 대해서 다루고자 한다.
Likelihood function and MLE
먼저 likelihood function은 다음과 같다 (n개의 joint PDF, independent and identically distributed (IID) 일때).

Log transformation을 하여 log-likelihood function도 존재한다.
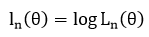
이때 MLE는 위 function을 maximize하는 theta 값이다. 만약 위 함수가 concave (위로 솟은 모양)이라면 theta로 미분했을 때 0이 되는 theta 값이 MLE가 된다.
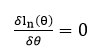
즉, likelihood function(parameter의 function)은 우리의 데이터를 생성했을 것 같은 parameter의 정도를 나타내는 함수이며, 위 과정은 이 함수를 최대로 하는 parameter를 찾아 MLE라고 하는 것이다.
MLE의 특징 1: Asymptotically optimal
최소한 consistent한 다른 estimator와 비교했을 때 MLE는 가장 작은 variance를 가진다.
예를 들어, 평균의 MLE는 sample mean인데, sample mean의 variance가 sample median의 variance보다 더 작다.
MLE의 특징 2: Asymptotically normal distribution
MLE는 n이 무한대로 갈 때, 아래와 같이 normal distribution을 따른다.

이때 theta hat이 우리가 parameter theta에 대해 예측한 MLE이다.
SE hat은 MLE의 standard error를 나타내는데, 이를 계산하기 위해서 score function과 Fisher information에 대한 개념을 짚고 넘어가면 좋다 (SE hat은 Fisher information으로 구할 수 있다).
Score function은 위에서 MLE를 구할 때 log-likelihood function을 theta로 미분했을 때 나온 식이고, Fisher information은 variance of score functions로 log-likelihood function을 theta로 두 번 미분한 식의 평균에 마이너스(정보가 음수가 되지 않도록)를 붙여주면 된다.

이 Fisher information은 중요한 의의를 가지는데, 일단 log-ikelihood function의 뾰족한 정도를 나타낸다. Function이 더 뾰족할수록 estimation이 잘 되었다고 할 수 있기 때문에 Fisher information이 클수록 estimator가 좋다고 할 수 있다. 또한 Fisher information을 통해 MLE의 variance를 estimate할 수 있다.
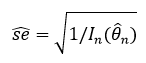
즉, Fisher information을 통해 MLE의 standard error를 구하면, 이를 통해 MLE의 분포를 알 수 있고, 신뢰구간 등을 만들어 볼 수 있다.
MLE의 특징 3: Equivalent
Equivalent라는 성질은 다음과 같은 뜻이다.
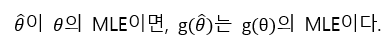
또 이와 관련된 개념으로 delta method가 존재하는데, 이는 theta의 분포가 아닌 theta를 포함한 함수의 분포를 구할 때 사용할 수 있다.
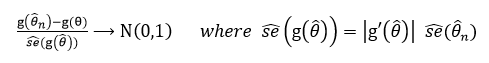
그 외에도 MLE는 unbiased esimator가 아니지만 consistent하다는 특징이 있다.
Reference
- Wasserman, L. (2004). All of Statistics: A concise course in statistical inference.
'Statistics' 카테고리의 다른 글
| [통계 기초] 표준 편차 (Standard deviation)와 표준 오차 (Standard error) 차이 (0) | 2021.06.29 |
|---|---|
| [통계 기초] Linear Regression (선형 회귀분석) & Logistic Regression (로지스틱 회귀분석) (0) | 2021.06.10 |
| [통계 기초] Bayesian Inference (베이즈 추론) (0) | 2021.05.25 |
| [통계 기초] ANOVA (분산 분석) (0) | 2021.05.23 |
| [통계 기초] Permutation test (0) | 2021.05.13 |