Bayesian Inference
먼저 확률에 대한 두 가지 학파가 존재한다: Frequentist VS Bayesian
- Frequentist는 확률을 빈도로 생각하며 (동전을 무한히 던졌을 때 앞면이 나올 frequency가 1/2), parameter에 대한 probability statements를 할 수 없다 (내가 평균 키보다 높을 확률은 30% 정도 되는 것 같아 X).
- 반면 Bayesian은 확률을 믿음의 정도(degree of belief)라고 생각하며, parameter에 대한 probability statements를 할 수 있다 (내가 평균 키보다 높을 확률은 30% 정도 되는 것 같아 O). 따라서 어느 정도 주관적이라고 할 수 있으며, 사람 뇌가 동작하는 방식과 유사하여 머신러닝에서도 주로 사용된다 (Prior belief를 가진 채 데이터를 봐서 belief를 업데이트)
Bayesian theory는 1700년대에 처음 나왔으며, 1800년대 statistics는 주로 Bayesian이었다. 그 후 1900년대에 되어서는Frequentist 위주로 바뀌었는데 (Fisher, Pierson), 그 이유 중 하나는 Bayesian의 경우 계산이 어려웠기 때문이다. 최근 들어서는 컴퓨팅 자원의 발달로 다시 Bayesian이 주목을 받게 됐다.
Bayesian Inference
Bayesian inference는 1) prior와 2) model, 3) data를 바탕으로 posterior pdf를 구하고, 최종적으로 posterior mean을 구하는 과정이다. Posterior pdf는 다음과 같다.

즉, posterior pdf는 데이터로부터 얻는 theta의 정보(모델)와 prior에서 얻는 theta의 정보를 모두 고려하는 것이다. 한편 posterior mean은 posterior pdf로부터 구할 수 있다.
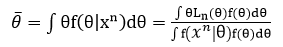
그런데 Bayesian은 종종 주관적이라는 이유로 공격 받는다. 즉, 우리가 prior를 어떻게 상정하는지에 따라 결과가 달라질 수 있다는 것이다. 그런 공격을 피하기 위해 non-informative prior를 사용할 수 있다. 그 종류에는 flat prior와 Jeffreys' prior가 있는데, 되도록 prior에 정보를 넣지 않기 위한 시도로 만들어졌다. 예를 들어, flat prior는 prior로 constant를 사용하는 방법이다.
Bayesian Testing
Frequentist 관점에서는 given data에서 null hypothesis의 확률을 계산할 수 없었지만 Bayesian에서는 가능하다.

이때 Bayes factor라는 개념이 존재하는데, 다음과 같다.
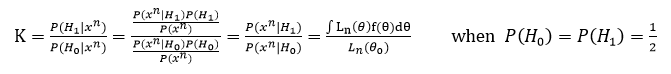
이 Bayes factor의 해석은 다음 링크 참조.
Bayes factor - Wikipedia
From Wikipedia, the free encyclopedia Jump to navigation Jump to search A statistical factor used to compare competing hypotheses In statistics, the use of Bayes factors is a Bayesian alternative to classical hypothesis testing.[1][2] Bayesian model compar
en.wikipedia.org
- Bayes factor의 좋은 점은 H1이 나올 확률과 H0이 나올 확률의 비율을 계산하기 때문에 직접적인 해석(H1의 확률이 100배 더 높다 등)이 가능하다는 점이다.
- 사람들이 이전까지 frequentist 관점에서 p-value만 굉장히 많이 사용하였지만, 이후 p-value와 Bayes factors와 연관시키려는 연구들이 계속 존재하였다.
- Frequentist의 p-value결과와 Bayesian의 Bayes factors가 다른 결과(해석)가 나올 수 있다. 어떤 것을 써야하는지는 여러 종보를 모아 종합적으로 판단하는 것이 맞을 듯.
Bayesain Computing
대부분의 경우 posterior distribution을 유도하기 어렵기 때문에 computational approach인 Markov-Chain Monte-Carlo (MCMC)가 사용된다. 그 예로는 Metropolis-Hastings algorithm과 Gibbs sampler가 있다.
Reference
- Wasserman, L. (2004). All of Statistics: A concise course in statistical inference.
'Statistics' 카테고리의 다른 글
| [통계 기초] Linear Regression (선형 회귀분석) & Logistic Regression (로지스틱 회귀분석) (0) | 2021.06.10 |
|---|---|
| [통계 기초] Maximum Likelihood Estimation (MLE) (0) | 2021.06.10 |
| [통계 기초] ANOVA (분산 분석) (0) | 2021.05.23 |
| [통계 기초] Permutation test (0) | 2021.05.13 |
| [통계 기초] Type 1 error와 Type 2 error (false positive와 false negative) (0) | 2021.04.28 |