Bootstrap (부트스트랩)
Bootstrap은 1970년대 후반에 개발되어 이후 통계학과 머신 러닝 등의 분야에서 광범위하게 이용되는 방법이다. Estimator의 분산 및 신뢰구간을 직접 구하기 힘들 때나, predictor의 성능을 높여주고자 할 때 사용할 수 있다 (Bootstrap 이용 예시 참조).
Bootstrap은 기존의 data set 1개에서 B번의 simulation을 통해 새로운 data set B개를 sampling하는 방법이다.
Bootstrap sampling 과정을 구체적으로 설명하면 다음과 같다.
X1부터 Xn까지 n개의 data point가 있다고 가정하자 (기존의 data set 1개). 각각의 data point가 나올 확률은 1/n이라고 생각한다 (empirical CDF, bootstrap의 이론적 배경). 이때 dataset에서 replacement를 허용하여 random하게 n개의 data point를 뽑아서 새로운 data set을 만든다 (replacement를 허용하지 않으면 순서만 바꾸는 permutation이 된다). 이를 B번 반복하면 B개의 새로운 data set이 생성된다.
Bootstrap 이용 예시
Bootstrap variance estimator
Estimator의 분산을 직접 구하기 힘들 때 bootstrap을 이용할 수 있다.
예를 들어, 어떤 분포에서 생성된 것인지 모르는 n개의 데이터가 있을 때 여기에서 sample median을 구할 수 있는데, sample median의 분산을 추정하는데 bootstrap을 사용할 수 있다. 이때 sample median은 population median에 대한 estimator이고, 이 estimator의 uncertainty를 측정하기 위해 분산을 구하는 것이다.
Bootstrap을 이용하지 않는다면 우리는 n개의 데이터로부터 1개의 sample median만 알 수 있다. 하지만 bootstrap sampling을 B번 반복하면 B개의 data set (각각의 n개의 data point를 가짐)이 생성되고, 이로부터 B개의 sample median을 구할 수 있다.
1) 이 B개 sample median의 분산을 구하면, 이를 이용해 2) 각각의 data point가 나올 확률은 1/n이라는 분포(empirical CDF)를 가정했을 때의 분산을 추정할 수 있고, 최종적으로는 3) 실제 분포를 가정했을 때의 분산을 추정할 수 있다.
즉, 우리는 3)의 분산을 구하기 위해 위 과정을 수행한 것이다.
위 과정에서 두번의 approximation이 적용된다. 첫 번째로 empirical CDF를 가정했을 때의 분산을 추정할 때 simulation 결과를 이용하였고, 두 번째로 실제 분포를 가정했을 때의 분산을 추정할 때 empirical CDF를 가정했을 때의 분산을 이용하였다. 일반적으로 첫 번째는 B를 늘리면 두 값이 유사해지지만, 두 번째의 경우 sample size가 작다면 차이가 있을 수 있다.
Bootstrap confidence interval
Estimator의 신뢰구간을 직접 구하기 힘들 때도 bootstrap을 사용할 수 있다.
2가지 방식을 소개하면 다음과 같다.
[Percentile interval]: B개의 bootstrap estimator를 구했다면, 특정 quantile에 해당하는 bootstrap estimator으로 신뢰구간을 나타내는 방식이다. 신뢰구간은 다음과 같다.

[Normal interval]: Statistics의 asymptotic distribution이 normal distribution을 따른다고 가정한다. 이때 standard error를 직접 구하기는 어렵기 때문에 bootstrap을 이용해서 구한다 (bootstrap variance estimator). 신뢰구간은 다음과 같다.
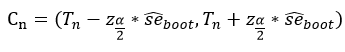
Bootstrap aggregating (Bagging)
Predictor의 성능을 높여주고자 할 때 bootstrap을 사용할 수 있다.
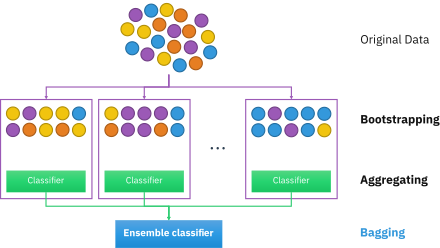
Bootstrap aggregating (Bagging)이란, 하나의 original data가 있을 때, B번의 bootstrap sampling을 통해 B개의 데이터를 새로 만들고, 이를 이용하여 B개의 classifier를 만들고 합치는 것을 말한다.
새로운 데이터가 오면 B개의 classifier에서 B개의 prediction이 생성되는데, 가장 주된 prediction이 무엇인지 voting하여 최종 결정을 내린다 (ensemble approach). Prediction accuracy(Performance)를 상당히 증가시켜 준다.
이 방법은 original data를 여러 batch로 나눈 뒤 각각에 대해 다른 classifier를 학습하는 것과는 다르다. Bootstrap을 쓰면 sample size를 n으로 쓰지만, batch로 나누면 sample size가 확 줄어드는 (subset만 이용) 차이가 있다.
특히 bootstrap을 이용하는 가장 유명한 방법 중 하나로 Random Forest가 있다. 이는 bagging으로 여러 tree를 만들어 training한 후, 새로운 데이터가 왔을 때 각각의 tree에서 예측한 결과에 대한 majority-voting을 통해 final class를 정하는 방법이다. 일반적으로 tree method (decision tree)는 해석이 편하며 직관적이라는 장점이 있는데 performance가 좋지 않다. 하지만 이들을 모아 forest를 만들면 performance를 높일 수 있어 그 단점이 보완된다.

Parametric bootstrap
위에서 다뤘던 (nonparametric) bootstrap이 분포에 대한 가정 없이 오직 데이터가 IID sample (independent identically distributed)이라는 가정만 있었다면, parameteric bootstrap에서는 분포에 대한 가정을 추가하여 정확도를 더 향상시키고자 하는 방법이다.
Parameteric bootstrap은 parametric inference와 bootstrap의 중간에 있는 hybrid라고 생각하면 좋다. Parametric inference는 분포를 가정했을 때 해당하는 parameter를 찾는 추론으로, 대표적인 방법으로 MoM (Method of Moments)과 MLE (Maximum Likelihood Estimation)가 있다. 이때 MLE는 1) asymptotical normality를 가지며 (n이 무한대로 갈 때 normal distribution을 가짐), 2) 최소 consistent한 다른 estimator와 비교해봤을 때 가장 variance가 작은 estimator이기 때문에 parameter inference에 주로 사용된다.
따라서 parametric bootstrap에서는 먼저 데이터가 주어졌을 때 분포를 가정한 후, 데이터를 이용하여 MLE를 구한다. 그러면 분포를 알수 있게 되는데 이를 true distribution function이라고 생각하여 이를 이용해서 B개의 data set (각각의 set는 n개의 데이터)를 생성할 수 있다. 생성된 data set에서 statistic T를 계산하면 B개의 T를 얻을 수 있고, 이를 이용하여 standard error나 confidence interval을 구할 수 있다.
Reference
- Wasserman, L. (2004). All of Statistics: A concise course in statistical inference.
'Statistics' 카테고리의 다른 글
| [통계 기초] Permutation test (0) | 2021.05.13 |
|---|---|
| [통계 기초] Type 1 error와 Type 2 error (false positive와 false negative) (0) | 2021.04.28 |
| [통계 기초] 표본평균의 분포 (sample mean distribution) (0) | 2021.04.20 |
| [통계 기초] 공분산과 상관 계수 (Covariance and Correlation) (0) | 2021.04.19 |
| [통계 기초] 신뢰 구간과 가설 검정, 유의 확률 (Confidence interval, Hypothesis testing, P-value) (0) | 2021.04.19 |