용어 정리
1. Sample space, Event, Outcome
확률에 대해 이해하기 전에 위 세 가지 개념을 먼저 이해하면 좋다.
Sample space는 모든 가능한 outcome의 집합이며, Event는 sample space의 subset이고, Outcome은 sample space의 element이다.
예를 들어, 동전을 두 번 던진다고 할 때, sample space={HH, HT, TH, TT}가 되고, 첫 번째 동전이 앞면일 사건 A (event)는 {HH, HT}이며, HH와 HT 각각이 outcome이라고 이해하면 쉽다.
2. 확률 (Probability distribution, Probability measure)
확률은 data generation process를 설명하는 언어이다. 반대로 관측된 data에서 data generation process를 추정하는 것이 inference/learning이라고 한다. 확률을 해석하는 두 가지 학파가 존재하는데, frequentist는 확률을 실험적으로 생각하며 Bayesian은 믿음의 정도로 생각한다.
확률은 event set을 받아서 숫자로 변환해주는 함수이며, 세 가지 공리를 만족해야 한다.
3. 확률 변수 (Random variable)
확률 변수는 outcome을 받아서 숫자로 변환해주는 함수이다. 수학적으로는 함수이지만 우리가 사용할 때는 variable처럼 쓰기 때문에 random variable이라고 한다.
4. 확률 함수 (Probability function)
확률 함수를 이용하여 '특정 값이나 특정 값의 범위를 갖는 확률 변수'의 확률을 계산할 수 있다.
확률 변수가 discrete인 경우, Probability mass function (PMF)을 정의할 수 있다. x에서의 PMF 값이 x를 가지는 확률 변수의 확률(P(X=x))이다.
반면, 확률변수가 continuous인 경우, Probability density function (PDF)을 정의할 수 있다. P(a<X<b)의 값은 PDF를 a부터 b까지 적분한 값이다.
참고로, Cumulative distribution function (CDF)는 x를 받아서 P(X<=x)를 반환하는 함수이다. 확률 변수의 모든 정보를 가지고 있으며, PMF와 PDF에서 생성할 수 있다.
이때, PMF와 CDF는 확률이지만, PDF는 확률이 아니다. PDF의 값은 1보다 큰 값이 될 수 있기 때문이다. PDF는 적분을 통해 확률을 구할 수 있게 해주는 weighting function이라고 이해하면 된다.
유명한 확률 변수
Descrete Random Varible
| Distribution | Notation | Probability function |
| Bernoulli distribution |  |
 |
| Binomial distribution |  |
en.wikipedia.org/wiki/Binomial_distribution |
| Geometric distribution | 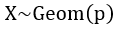 |
en.wikipedia.org/wiki/Geometric_distribution |
| Poisson distribution |  |
en.wikipedia.org/wiki/Poisson_distribution |
Continous Random Variable
| Distribution | Notation | Probability function |
| Normal distribution |  |
en.wikipedia.org/wiki/Normal_distribution |
| Chi-squared distribution |  |
en.wikipedia.org/wiki/Chi-square_distribution |
| Exponential distribution |  |
en.wikipedia.org/wiki/Exponential_distribution |
Reference
- Wasserman, L. (2004). All of Statistics: A concise course in statistical inference.
'Statistics' 카테고리의 다른 글
| [통계 기초] 신뢰 구간과 가설 검정, 유의 확률 (Confidence interval, Hypothesis testing, P-value) (0) | 2021.04.19 |
|---|---|
| [통계 기초] 평균 제곱 오차 (Mean square error, MSE) (0) | 2021.04.19 |
| [통계학] Multiple Testing Correction의 필요성과 방법 (0) | 2021.03.24 |
| [t-test] R 코드와 함께 알아보는 t-검정 (One sample t-test, Paired t-test, Two sample t-test) (0) | 2021.03.23 |
| [통계학] 특정 상황 별 적용 가능한 통계 기법 정리 (생명과학 실험, 생물정보학) (2) | 2021.02.15 |